Problem #125
Tags: graph theory
What is the out-degree of node \(u\) in the graph shown below?
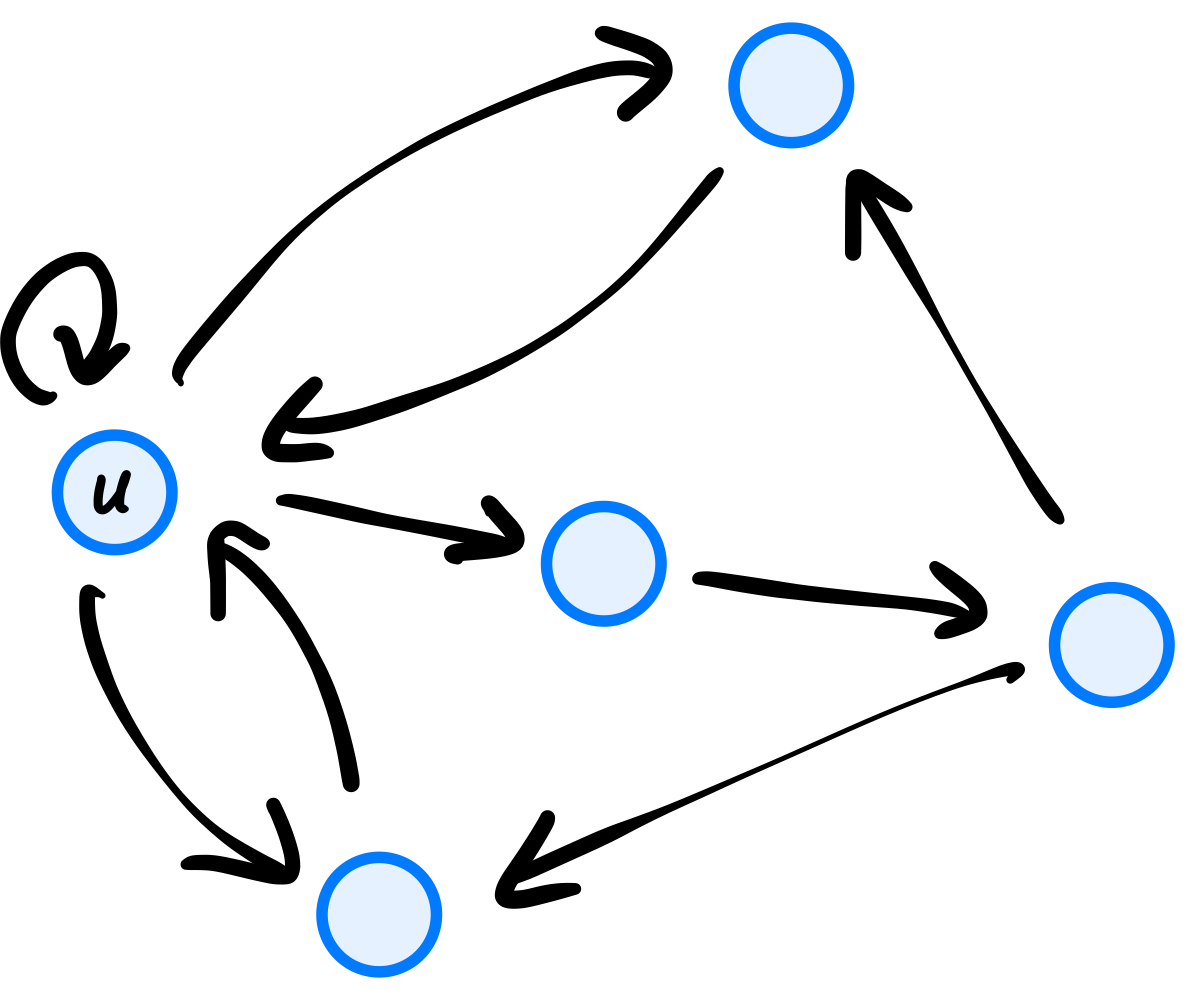
Solution
4
Tags: graph theory
An undirected graph has 5 nodes. What is the greatest number of edges it can have?
10
Tags: graph theory
A directed graph has 10 edges. What is the smallest number of nodes it can have?
4
Tags: connected components, graph theory
An undirected graph with 20 nodes and 30 edges has three connected components: \(A\), \(B\), and \(C\). Connected component \(A\) has 7 nodes. What is the smallest number of edges it can have?
6
Tags: graph theory
Let \(v = \{a, b, c, d, e, f, g\}\) and \(E = \{(a,g), (b,d), (d, e), (f, d)\}\). How many connected components does the undirected graph \(G =(V, E)\) have?
3
Tags: graph theory
Let \(G = (V, E)\) be a directed graph with \(|V| > 1\). Suppose that every node in \(G\) is reachable from every other node. True or False: each node in the graph must have an out-degree of at least one and an in-degree of at least one.
True.
Tags: graph theory
An undirected graph \(G = (V, E)\) has 23 nodes and 2 connected components. What is the smallest number of edges it can have?
21
Tags: connected components, graph theory
Let \(G = (V, E)\) be an undirected graph, and suppose that \(u, v, \) and \(w\) are three nodes in \(V\). Suppose that \(u\) and \(v\) are in the same connected component, but \(u\) and \(w\) are not in the same connected component. True or False: it is possible that \(v\) and \(w\) are in the same connected component.
False.
Tags: graph theory
Let \(G\) be an undirected graph. Suppose that the degree of every node in the graph is greater than or equal to one. True or False: \(G\) must be connected.
False.
Tags: graph theory
What is the out-degree of node \(u\) in the graph shown below?

4
Tags: graph theory
Suppose \(u\) is a node in a complete, undirected graph \(G = (V,E)\). What is the degree of \(u\)? Remember, an undirected graph is complete if it contains every possible edge.
\(|V| - 1\)
Tags: graph theory
Let \(V = \{a, b, c, d\}\) and \(E = \{(a,b), (a,a), (a,c), (d,b), (c,a)\}\) be the nodes and edges of a directed graph. How many predecessors does node \(b\) have?
2
Tags: connected components, graph theory
Let \(C\) be a connected component in an undirected graph \(G\). Suppose \(u_1\) is a node in \(C\) and let \(u_2\) be a node that is reachable from \(u_1\). True or False: \(u_2\) must also be in the same connected component, \(C\).
True.
Tags: graph theory
Let \(G = (V, E)\) be a connected, undirected graph with 16 nodes and 35 edges. What is the greatest possible number of edges that can be in a simple path within \(G\)?
15
Tags: connected components, graph theory
Suppose \(G = (V, E)\) is an undirected graph. Let \(k\) be the number of connected components in \(G\). True or False: it is possible that \(k > |E|\).
True.
Tags: graph theory
Let \(G = (V, E)\) be a directed graph, and suppose \(u, v, w \in V\) are all nodes. True or False: if \(w\) is reachable from \(v\), and \(v\) is reachable from \(u\), then \(w\) is reachable from \(u\).
True.
Tags: graph theory
Let \(G = (V,E)\) be a connected, undirected graph with \(|E| = |V| - 1\). Suppose \(u\) and \(v\) are both nodes in \(G\). True or False: there can be more than one simple path from \(u\) to \(v\).
False.
Tags: connected components, graph theory
Suppose an undirected graph \(G = (V,E)\) has two connected components, \(C_1\) and \(C_2\). Suppose that \(|C_1| = 4\) and \(|C_2| = 3\). What is the largest that \(|E|\) can possibly be?
Answer: 9. To load a graph with the most edges, make each connected component "fully connected". The most edges we can put in a component with 4 nodes is \(4 * 3 / 2 = 6\), and the most we can put into a component with 3 nodes is \(3 * 2 / 2 = 3\). Therefore, we can put at most 9 edges in this graph.